선형회귀란?
선형회귀(linear regression) 는 “변수들 사이의 관계를 직선(linear)으로 표현하는 통계적 방법”입니다.
쉽게 말해, 어떤 요인이 결과에 얼마나 영향을 주는지를 수학적으로 설명하려는 모델입니다.
예를 들어,
- 공부시간이 늘어나면 점수가 얼마나 오를까?
- 몸무게가 늘면 기초대사량은 얼마나 변할까?
이런 관계를 ‘직선 하나로’ 나타내는 게 선형회귀의 핵심입니다.
왜 ‘선형(linear)’이라고 부를까?
‘선형’이라는 말은 직선 관계(linear relationship) 를 뜻합니다.
결과값 가 입력값 의 1차 함수 형태로 나타난다는 의미합니다.

- : 종속변수(결과, 우리가 예측하고 싶은 값)
- : 독립변수(설명변수, 결과에 영향을 주는 요인)
- β0: 절편(intercept). x=0일 때 y의 값
- β1: 기울기(slope). x가 1 단위 변할 때 y가 얼마나 변하는가
- ε: 오차(error). 모델이 설명하지 못하는 부분
이때 β0,β1 값을 찾아주는 게 회귀(regression) 의 핵심입니다.
초등학생 때 y=ax+b에서 점 2개 나왔을 때 a, b 구했던거 생각하면 이해하기 쉬울 것 같습니다.
‘회귀(regression)’라는 말의 유래
‘회귀’라는 단어는 “회귀선(regression line)” 이라는 말에서 왔습니다.
영국의 통계학자 프랜시스 골턴(Francis Galton) 이 19세기 후반에
“부모의 키가 클수록 자녀의 키도 크지만, 완벽히 비례하지는 않고 평균 쪽으로 ‘회귀(regress)’한다”는 연구에서 처음 사용했습니다.
이때 ‘평균으로 돌아간다(regression to the mean)’는 표현이 통계학 용어로 자리 잡았고,
이후 직선 관계를 찾는 모든 분석법을 ‘회귀분석(regression analysis)’ 이라 부르게 되었습니다.
단순선형회귀 vs 다중선형회귀
| 단순선형회귀(Simple Linear Regression) | 독립변수가 1개인 경우 | 공부시간 → 점수 |
| 다중선형회귀(Multiple Linear Regression) | 독립변수가 여러 개인 경우 | 공부시간 + 수면시간 + 과외시간 → 점수 |
즉, 단순선형회귀는 하나의 요인만 고려하지만,
다중선형회귀는 여러 요인의 영향을 동시에 분석합니다.
선형회귀의 목적
- 예측(Prediction)
→ 새로운 값에 대해 값을 예측하기 위해 - 관계 파악(Explanation)
→ 변수 간의 관계(예: x가 y에 얼마나 영향을 주는가)를 수치로 표현하기 위해
즉, “미래를 예측”하거나 “현상을 설명”하는 데 모두 쓰입니다.
선형회귀로 얻을 수 있는 것
(1) 회귀식 (Regression Equation)
데이터를 가장 잘 설명하는 직선:
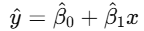
이 식이 바로 ‘예측식’ 이 됩니다.
(2) 신뢰도(유의성 검정)
기울기 β1이 통계적으로 의미 있는 관계인지 확인합니다.
p-value(유의확률)가 0.05보다 작으면 “x와 y 사이에 유의한 관계가 있다”고 해석합니다.
(3) 설명력(결정계수, R²)

R²는 모델이 데이터를 얼마나 잘 설명하는지를 나타내며,
0~1 사이의 값으로, 1에 가까울수록 설명력이 높다는 뜻입니다.
직관적으로 이해하기
데이터 점들을 그래프에 찍었을 때, 그 사이를 가장 잘 통과하는 직선(fitted line) 을 그리는 게 선형회귀입니다.
이 직선과 실제 점들 사이의 세로 거리(오차)가 가장 작아지도록 계산합니다.
즉, “오차 제곱합이 최소가 되는 직선”을 찾는 게 선형회귀의 핵심 원리입니다.
'프로그래밍 언어 문법 및 개념 > R' 카테고리의 다른 글
| 📊R - 상관계수 (0) | 2025.11.01 |
|---|---|
| 📊R – 연산 기호, 함수, 그리고 분포 기초 정리 (0) | 2025.10.11 |
| 📊R – 기본 개념과 첫 코드 실행 (0) | 2025.09.27 |

