목차
특정 학과에서 전공필수 과목 중 파이썬, R 이렇게 두 과목이 있다고 합시다.
학생들의 파이썬 성적을 X, R성적을 Y라고 하면, 두 개의 분포가 어떤 관련이 있는지 궁금할 것 입니다.
이를 알려주는 두 개의 통계량이 공분산과 상관계수입니다.
ex) 파이썬 잘 본사람은 R도 잘 봤나?
Covariation(공분산)
확률변수X, Y가 존재하고 (X= x₁, x₂, …, xₙ)
여기서 확률변수X, Y에 대하여 공분산은 Cov(X, Y)이고
Cov(X, Y) = E[(X-E(X))(Y-E(Y))] 로 정의합니다. (E(X): X들의 평균)
전개하면 E[XY] - E[X]E[Y] 입니다.
편차들의 제곱의 평균인 분산, Var(X) = E[(X-E(X))^2]과 비슷하게 생긴 것을 알 수 있는데
실제로 Cov(X, X) = Var(X)입니다.
공분산이 양수이면 X, Y가 비례하는 경향이란 것을 알 수 있습니다. (비율이 일정한게 아니라서 비례관계가 아닌, 비례 경향)
반대로 공분산이 음수이면 반비례 관계 경향이 있다고 할 수 있습니다.
X, Y가 독립적인 관계일 땐 공분산이 0(관련성 0)입니다.
요약
확률변수X, Y에 대하여 Cov(X, Y)을 공분산이라 합니다.
- 두 변수 X, 가 같은 방향으로 움직이면 Cov(X,Y)>0
- 반대 방향이면 Cov(X,Y)<0
- 서로 무관하면 Cov(X,Y)≈0 그러나 Cov(X,Y)=0이라고 해서 X, Y가 독립이라고 할 수는 없습니다.
Correlation(상관계수)
여기서 두 분포의 상관계수는 다음과 같이 정의됩니다.

여기서 아래와 같은 범위를 구할 수 있는데 증명은 생략하겠습니다.
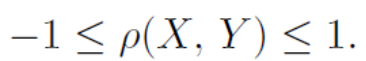
상관계수가 1에 가까울수록 강한 양의 상관관계에 있다고 말하고 -1에 가까울수록 강한 음의 상관관계에 있다고 말합니다.

산점도로 보면 위 그림과 같습니다.
중3 2학기 마지막 단원에 이 산점도와 상관계수를 다루던데 이런 걸 배웠었구나 싶었습니다. (2015개정 때 도입된 개념으로 추정)
상관계수는 공분산과 다르게 확실하게 선형 비례관계입니다. (일정 비율 관계)
공분산은 클수록 상관 관계가 높은게 아닙니다. 맞을 때도 많지만 단위 차이가 많이나는 경우엔 실제로 상관 관계와 상관없이 더 높게 나옵니다.
하지만 상관계수는 공분산과 다르게 높을수록 상관 관계가 높은 것이기에 더 유용합니다.
다음으로 상관 분석을 설명하기전에 귀무가설에 대해 알아보겠습니다.
귀무가설 (Null Hypothesis, H₀)
귀무가설 H₀ 은 “변화나 차이가 없다”는 가정입니다.
대립가설 H₁ 은 이와 반대되는 개념입니다. 예시는 아래와 같습니다.
| 상황 | 귀무가설 H₀ | 대립가설 H₁ |
| 약의 효과를 검정 | “이 약은 효과가 없다” | “이 약은 효과가 있다” |
| 두 집단 평균 비교 | “두 집단의 평균이 같다” | “두 집단의 평균이 다르다” |
| 상관계수 검정 | “상관관계가 없다 (ρ=0)” | “상관관계가 있다 (ρ≠0)” |
추가적으로 따라오는 개념인 유의수준과 p-value를 설명하자면
유의수준(Significance Level, α)
귀무가설을 ‘틀렸다고 판단할 기준선’입니다.
보통 α = 0.05 (5%) 를 가장 자주 씁니다.
뜻은 이렇게 해석됩니다:
“실제로는 차이가 없는데도,
우리가 우연히 5% 확률로 ‘차이가 있다’고 잘못 결론 내릴 수 있다.”
즉, 오판을 허용하는 최대 확률입니다.
여기서 오판은 귀무가설이 사실인데도, 그것을 기각해버리는 잘못된 판단(대립가설)입니다.
즉, 어떤 드문 일이 일어날 확률이 유의수준 이내이면 차이가 있다고 판단하는 것입니다.
예시로 이해하는게 편한 것 같습니다.
예시: 어떤 약의 효과가 있는지 실험을 진행했다.
실험한 약으로 완치율은 10%였고, 가짜약의 완치율은 8%였다.
2%차이가 실험한 약이 약효가 없어도 우연히 일어날 확률(즉, 둘 다 약효가 없는 약이라 우연한 개인 차이)이 유의수준 이하이면 2%차이도 일어나기 드문 일이라 약효가 있다고 대립가설을 채택하는 것이다.
p-value(유의확률)
p값: ‘H₀가 맞다면 이런 결과가 나올 확률’ (유의수준 파트 예시에서 2%차이가 일어날 확률에 해당함.)
위 세 가지 개념(귀무가설, 유의수준, p값)으로 표현할 수 있는 것은
p-value가 유의수준보다 낮으면 귀무가설은 기각하고 대립가설이 맞다고 보는 것입니다.
예를 하나 더 들자면 동전은 공평하다고 가정하고 유의수준을 5%로 설정합시다. 동전 10번을 던졌을 때 모두 앞면이 나온다면 약 0.01% 수준의 사건이 발생한 것이므로 너무 드문일입니다. 따라서 운이 좋다기보다는 동전은 편향적이라고 봅니다.
여기까지 상관관계관련 개념에 대해 나열해보았습니다.
'프로그래밍 언어 문법 및 개념 > R' 카테고리의 다른 글
| 📊R - 단순선형회귀 (Simple Linear Regression) (0) | 2025.11.08 |
|---|---|
| 📊R – 연산 기호, 함수, 그리고 분포 기초 정리 (0) | 2025.10.11 |
| 📊R – 기본 개념과 첫 코드 실행 (0) | 2025.09.27 |

