목차
오늘은 R의 가장 기본이 되는 연산 기호, 함수, 그리고 확률분포를 정리해보겠습니다.
연산 기호
%%: 나머지 연산자. 7%%3은 1이 출력됨.
%/%: 정수나눗셈의 정수 몫 반환. 7%/%3은 2가 출력됨.
%*%: 행렬 곱셈
%in%: 왼쪽이 오른쪽의 원소이면 TRUE, 아니면 FALSE 반환. c(1, 2, 3) %in% c(2, 3, 4)은 FALSE TRUE FALSE라고 나옴.
!: 논리 부정. 수학에서도 똑같이 쓰이는 부호. 5!: 5가 아닌
연산 함수
log(4, 2): 밑을 2로하는 로그
asin(1/2): arcsin 함수(미분적분학1에 나옴)
sqrt(4): 4의 제곱근
fastorial(5): 5!
choose(10, 5): 서로 다른 10개에서 3개를 선택하는 조합의 수
abs(-10): 절대값
함수 정의
예시보면서 배우기.
cv <- function(x) mean(x)
이런 식으로 cv에 mean(x)라는 함수를 정의해줄 수 있다. cf, mean(x)는 평균을 구하는 연산 함수이다.
weight <- c(120, 80) 라고 정의한 뒤 x자리에 대입하려면
cv(weight)라고 입력하면 된다.
그럼 120과 80의 평균인 100이 나온다.
여기까지는 R언어에서 이런 것들을 출력하는 것이 있구나~ 하고 이과면 평소에 많이 접하기도 해서 친숙할 것이라고 생각합니다.
이 다음은 통계 관련 개념들을 많이 다룰 것인데 확률분포부터 다뤄보겠습니다.
확률 분포
확률분포란 어떤 사건이나 값이 일어날 가능성이 어떻게 퍼져 있는지를 나타내는 규칙으로,
데이터가 어떤 형태로 분포되는지 분석하거나 미래 결과를 예측할 때 사용됩니다.
확률분포는 이산적(끊긴 상태)인지 연속적인지에 따라 크게 두 가지로 나뉩니다.
대표적인 확률 분포를 살펴보겠습니다.
(아래 그래프들은 형태보여주기용이고 임의의 (x, y)입니다.)
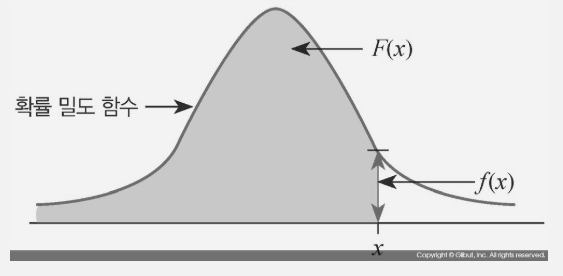
누적 분포 함수(cumulative distribution function)를 F(x)라 하면 F(x) = P{X ≤ x}로 정의되는 것으로 어떤 확률변수X가 x이하일 확률을 말한다. 예시로 주사위 눈 특정 개수 이하일 확률 등이 있습니다.
왼쪽은 0 오른쪽은 1에 수렴. S자 형태.

확률밀도함수(PDF)란 연속형 확률변수가 어떤 값을 가질 가능성의 밀도(농도)를 나타내는 함수입니다.
즉, “특정 구간에 값이 존재할 확률이 얼마나 되는가”를 알려주는 함수입니다.
연속확률밀도함수가 연속이라면 누적 분포 함수를 미분하면 확률밀도 함수(연속확률밀도함수)를 얻습니다. 그러므로 확률밀도함수는 적분하면(면적은) 누적 분포 함수입니다.
이산 균등분포(discrete uniform distribution)란 서로 다른 몇 개의 값이 모두 같은 확률로 발생하는 분포를 말합니다.
모든 수가 나올 확률이 같은 주사위가 대표적인 예입니다.
이항분포(binomial distribution)란 성공/실패처럼 두 가지 결과만 있는 시행을 여러 번 반복할 때, 성공의 개수가 따르는 분포입니다. n번의 독립된 시행에서 각 시행이 성공할 확률이 p일 때 성공 횟수 X가 따르는 분포를 이항분포 B(n, p) 라고 합니다.

다음은 이항분포에서 위 함수의 함수값을 의미하는 함수입니다.
dbinom(성공횟수, 시행횟수, 1회 성공확률) = 시행횟수 중 특정 횟수만큼 성공할 확률. 이항분포의 확률밀도 함수
pbinom(성공횟수 기준, 시행횟수, 1회 성공확률, lower.tail = TRUE/FALSE) = 시행횟수 중 특정 횟수 이하(초과)만큼 성공할 확률. 이항분포의 누적밀도함수
- lower.tail = TRUE 이면 성공횟수 기준 이하일 때 확률들의 합, 예를 들어 2번이하 = 0, 1, 2번 했을 때 확률의 합을 뜻합니다.
- lower.tail = FALSE 이면 성공횟수 기준 초과일 때 확률들의 합을 뜻합니다.
다른 분포로는 포아송 분포 등이 있습니다.
포아송분포(Poisson Distribution)란 단위 시간안에 어떤 사건이 몇번 발생할지 나타내는 확률 분포입니다,
비교적 발생확률이 적고 많은 시행이 일어날 때 사용합니다.
'프로그래밍 언어 문법 및 개념 > R' 카테고리의 다른 글
| 📊R - 단순선형회귀 (Simple Linear Regression) (0) | 2025.11.08 |
|---|---|
| 📊R - 상관계수 (0) | 2025.11.01 |
| 📊R – 기본 개념과 첫 코드 실행 (0) | 2025.09.27 |
